Las series numéricas son secuencias ordenadas de números que siguen un patrón específico. Son un concepto fundamental en matemáticas, con aplicaciones que abarcan desde la estadística y el análisis matemático hasta la programación y las ciencias aplicadas.

En este artículo, exploraremos qué son las series numéricas, cómo clasificarlas y ejemplos prácticos para una comprensión más profunda.

¿Qué Son las Series Numéricas?

Una serie numérica es una secuencia de números ordenados de acuerdo con una regla o fórmula. Los elementos de una serie se denominan términos. Cada término tiene una posición específica dentro de la serie, conocida como índice. Por ejemplo, en la serie 2,4,6,8,102,4,6,8,10, cada número es un término y la posición de cada número es su índice (1, 2, 3, 4, 5 respectivamente).

Diferencia Entre Series y Sucesiones

Es importante distinguir entre series y sucesiones. Una sucesión es simplemente una lista ordenada de números. Cuando sumamos los términos de una sucesión, obtenemos una serie. Por ejemplo, la sucesión 1,2,3,4,…1,2,3,4,… tiene una serie asociada 1+2+3+4+…1+2+3+4+….

También te puede interesarEl método loc en Python

Clasificación de las Series Numéricas

Las series numéricas se pueden clasificar de diversas maneras, según el criterio utilizado. Algunas de las clasificaciones más comunes incluyen:

Series Aritméticas

En una serie aritmética, la diferencia entre términos consecutivos es constante. Esta diferencia se denomina razón o diferencia común. Por ejemplo, en la serie 3,7,11,15,…3,7,11,15,…, la diferencia común es 44.

La fórmula del término general al n-ésimo de una serie aritmética es:

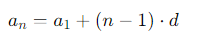
Donde:

• an​ es el término n-ésimo.
• a1​ es el primer término.
• d es la diferencia común.
• n es la posición del término.

Series Geométricas

En una serie geométrica, el cociente entre términos consecutivos es constante. Este cociente se denomina razón. Por ejemplo, en la serie 2,6,18,54,…2,6,18,54,…, la razón es 33.

También te puede interesarQlik Sense y sus ventajas en el análisis de datos

La fórmula del término general ?n-ésimo de una serie geométrica es:

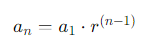
Donde:

• an​ es el término n-ésimo.
• a1​ es el primer término.
• r es la razón.
• n es la posición del término.

Series Armónicas

En una serie armónica, los términos son el recíproco de una serie aritmética. Por ejemplo, la serie 1,12,13,14,…1,21​,31​,41​,… es una serie armónica.

La fórmula del término general n-ésimo de una serie armónica es:

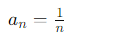
Series de Fibonacci

La serie de Fibonacci es una serie donde cada término es la suma de los dos términos anteriores. La serie comienza con 0,10,1 y se desarrolla como 0,1,1,2,3,5,8,…0,1,1,2,3,5,8,….

También te puede interesarCómo usar la fórmula BUSCARV en Power BI

La fórmula del término general ?n-ésimo de la serie de Fibonacci es:

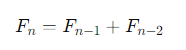
Donde:

• Fn​ es el término ?n-ésimo.
• Fn−1​ es el término anterior.
• Fn−2​ es el término dos posiciones atrás.

Ejemplos Prácticos en Programación

Para ilustrar cómo manejar series numéricas en programación, utilizaremos Python debido a su simplicidad y popularidad.

Serie Aritmética en Python

pythonCopiar códigodef serie_aritmetica(a1, d, n):
    return [a1 + (i - 1) * d for i in range(1, n + 1)]

# Ejemplo
a1 = 3
d = 4
n = 10
print(serie_aritmetica(a1, d, n))

Serie Geométrica en Python

pythonCopiar códigodef serie_geometrica(a1, r, n):
    return [a1 * (r ** (i - 1)) for i in range(1, n + 1)]

# Ejemplo
a1 = 2
r = 3
n = 10
print(serie_geometrica(a1, r, n))

Serie Armónica en Python

pythonCopiar códigodef serie_armonica(n):
    return [1 / i for i in range(1, n + 1)]

# Ejemplo
n = 10
print(serie_armonica(n))

Serie de Fibonacci en Python

pythonCopiar códigodef serie_fibonacci(n):
    fib = [0, 1]
    for i in range(2, n):
        fib.append(fib[-1] + fib[-2])
    return fib[:n]

# Ejemplo
n = 10
print(serie_fibonacci(n))

Aplicaciones de las Series Numéricas

Las series numéricas tienen aplicaciones en diversos campos, como la economía, la física, la biología y la informática. Algunas aplicaciones comunes incluyen:

• Análisis Financiero: Las series temporales de datos financieros, como precios de acciones y tasas de interés, pueden modelarse y analizarse utilizando series numéricas.
• Procesamiento de Señales: En ingeniería, las series numéricas se utilizan para analizar y procesar señales digitales.
• Algoritmos de Búsqueda y Ordenación: En informática, muchos algoritmos de búsqueda y ordenación utilizan series numéricas para optimizar su rendimiento.

Las series numéricas son una herramienta fundamental en matemáticas y ciencias aplicadas, proporcionando un marco para analizar y modelar fenómenos complejos. Su clasificación en series aritméticas, geométricas, armónicas y de Fibonacci permite una mejor comprensión de sus propiedades y aplicaciones.

Además, con el uso de lenguajes de programación como Python, es posible implementar y analizar estas series de manera efectiva, lo que amplía sus aplicaciones en diversos campos.

Con este conocimiento, puedes explorar más a fondo el mundo de las series numéricas y su impacto en diferentes disciplinas.